Больцмана статистика

Б про льцмана стат і стіки, фізична статистика для систем з великого числа невзаимодействующих частинок. Строго Б.с. підкоряються атомні і молекулярні ідеальні гази, т. е. гази, у яких потенційна енергія взаємодії молекул вважається рівною нулю. Реально до таких систем відносяться розріджені гази, молекули яких слабо взаємодіють один з одним.

При великому числі часток в системі неможливо детально описати поведінку кожної частки. Однак загальні риси поведінки системи в цілому є усередненими відображенням руху окремих частинок. Частинки розподіляються по можливим для них станів - їх координати r і імпульси р приймають певні значення. Математично це описується функцією розподілу, що характеризує ймовірність перебування частки в даному стані.

Для ідеального газу молекул, що знаходяться в полі зовнішніх сил, функція розподілу Больцмана має вигляд:

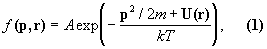
де р 2 / 2m - кінетична енергія молекули маси m, U (r) - її потенційна енергія в зовнішньому полі, k - Больцмана постійна , Т - абсолютна температура газу; постійна А визначається з умови, що сумарна кількість частинок, розподілених по всіх можливих станів, так само повного числа частинок в системі (умова нормування). Так як величина kT характеризує середню енергію теплового руху молекули, то в Б. с. розподіл часток по станах визначається відношенням повної енергії частинки (кінетична плюс потенційна) до енергії її теплового руху.

Функція розподілу (1) містить два співмножники: ехр (- р 2/2 mкТ) і exp (- U (r) / kT). Перший з них визначає розподіл молекул по імпульсам (або швидкостям), т. Е. Є Максвелла розподілом , А другий - розподіл за координатами в поле зовнішніх сил. Тому іноді тільки другу залежність називають розподілом Больцмана, а формулу (1) називають розподілом Максвелла - Больцмана.

За допомогою функції розподілу Больцмана легко отримати формулу зміни концентрації молекул повітря (незалежно від їх імпульсу) зі зміною висоти над земною поверхнею, а отже, і барометрическую формулу , Що визначає залежність тиску повітря від висоти.

У квантової статистики замість функції розподілу розглядається середнє число часток 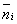, Що знаходяться в даному квантовому стані з енергією E i, і розподіл Больцмана виглядає наступним чином:

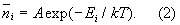
Постійна А знаходиться з умови

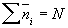
де N - загальне число частинок в системі, і дорівнює А = (N / V) (h2 / mkT) 3/2 (V - об'єм газу, h - планка постійна ). Розподіл (2) є граничним випадком квантових статистик Бозе - Ейнштейна і Фермі - Дірака, коли можна знехтувати квантовомеханічними ефектами, пов'язаними з взаємним впливом тотожних частинок (див. тотожності принцип ). Воно справедливо для систем, у яких все числа 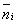малі в порівнянні з 1; це означає, що частинки проводять майже весь час в сильно розрізняються станах і тому специфічний вплив їх один на одного не проявляється.

Квантова Б. с. справедлива при малих щільності газу N / V і високих температурах (при даній масі часток). Фактично Б. с. застосовна для всіх розріджених молекулярних газів, тому що маса молекул велика і квантове вплив тотожних часток один на одного мало б проявитися лише при настільки високій щільності і низьких температурах, які відповідають твердому (для гелію - рідкому) стану речовини (а в цьому випадку Б. с. взагалі непридатна, т.к . взаємодія молекул велике). До електронного газу в металах і газу світлових квантів - фотонів - Б. с. непридатна (див. статистична фізика ).

Літ. см. при ст. статистична фізика .

В. П. Павлов.