Дангян А.Е. Хвильова функція електрона

Бібліографічна посилання на цю статтю:
Дангян А.Е. Хвильова функція електрона // Сучасні наукові дослідження та інновації. 2016. № 1 [Електронний ресурс]. URL: http://web.snauka.ru/issues/2016/01/62782 (дата звернення: 25.03.2019).

Вступ

Основним рівнянням, з якого витікала гіпотеза Луї де Бройля про хвильових властивості матерії, була формула, записана ним на підставі гіпотези Планка про найменшому квант енергії і рівняння Ейнштейна, що зв'язує масу і енергію, 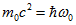. З неї випливало, що кожної порції енергії, що володіє масою 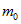, Відповідає періодичний процес, частота якого дорівнює .

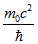Застосування гіпотези де Бройля до елементарних частинок, зокрема до електрону, означатиме, що електрон містить внутрішній хвильової процес. Але свого часу цей хвильовий процес не був виявлений і хвилі де Бройля стали асоціюватися тільки з механічним рухом частинок.

Сучасна фізика інтерпретує хвилі де Бройля як хвилі ймовірності, що не мають матеріального втілення.

Останнім часом, з'явилися експериментальні факти, що підтверджують первісну гіпотезу де Бройля про існування хвиль матерії [3], [4].

Ці експериментальні результати стимулювали появу численних спроб теоретичного пояснення [7], [8].

У даній роботі, шляхом вирішення релятивистского рівняння М2 [2] буде показано, що елементарні частинки, зокрема електрон, цілком можуть містити хвильової процес з досить специфічними властивостями. Хвильова модель нерухомого електрона представляється у вигляді сферичного хвильового процесу.

Дану статтю можна скачати у форматі PDF за посиланням - http://portalnp.ru/wp-content/uploads/2016/01/VolnovayaFunkciaElektrona1.pdf

Нестаціонарне рівняння М2

Перетворимо отримане в роботі [2] стаціонарне релятивістське рівняння М2 (1.1) в нестаціонарну форму.

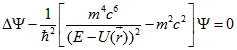(1.1)

Для цього видаляємо з рівняння потенційну енергію 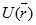і підставляємо залежне від часу і хвильової функції значення квадрата енергії 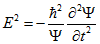в рівняння.

В результаті отримаємо: 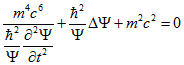(1.2)

Тепер необхідно знайти дисперсійне співвідношення для отриманого рівняння (1.2).

Для цього підставимо сферичну хвилю 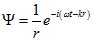(1.3) в рівняння.

Визначився другий похідне за часом: 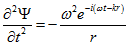(1.4)

Оператор Лапласа в сферичній системі координат має такий вигляд:

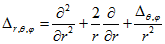(1.5)

Визначимо результат дії оператора Лапласа на сферичну хвилю:

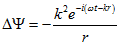(1.6) Підставимо сферичну хвилю (1.3) і отримані значення (1.4) і (1.6) у вихідне нестаціонарне рівняння (1.2).

В результаті отримаємо дисперсійне співвідношення у вигляді: 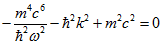(1.7)

Хвиля без дисперсії і хвильової пакет без распливанія

Для отриманого дисперсійного співвідношення, визначимо фазову і групову швидкості поширення хвиль.

Як відомо фазова швидкість визначається через кругову частоту 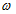і хвильове число 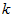за формулою: 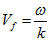(2.1)

З рівняння (1.7) визначимо кругову частоту 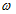. 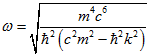(2.2)

Підставами отримане значення (2.2) в формулу (2.1) 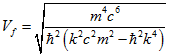(2.3)

Групова швидкість визначається за формулою: 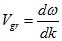(2.4). Визначимо похідну користуючись формулою (2.2). 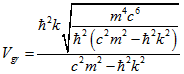(2.5).

Побудуємо графіки залежності фазової і групової швидкостей від хвильового числа 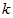. Далі будемо користуватися атомної системою одиниць Хартрі.

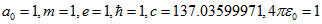
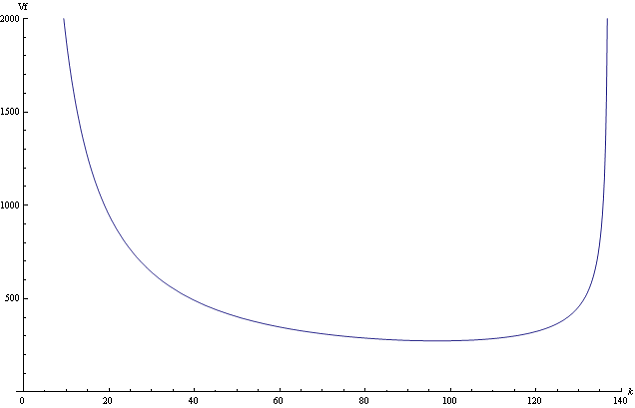
Рис.1 Графік залежності фазової швидкості 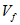від хвильового числа .

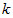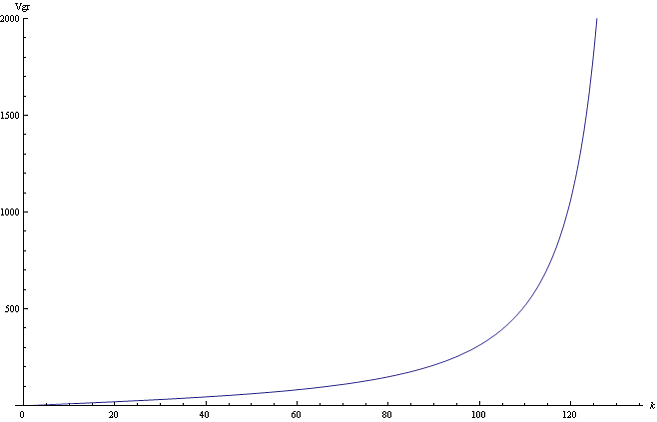
Рис.2 Графік залежності групової швидкості 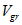від хвильового числа .

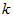Тепер сумісний обидва графіка на одному малюнку.

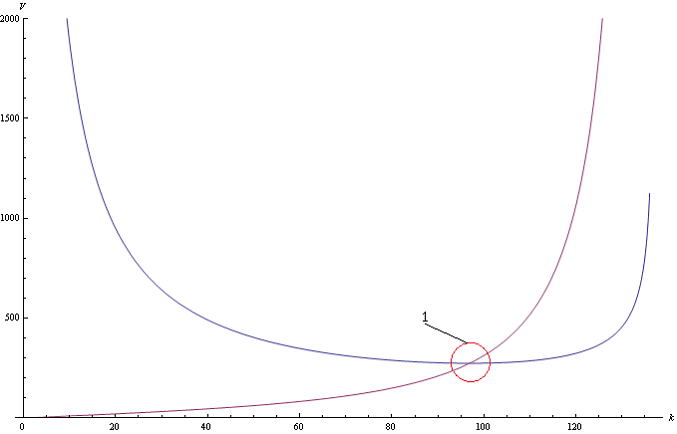
Рис.3 Спільний графік фазового і групового швидкостей.

Як можна помітити, при певному значенні хвильового числа, фазова швидкість дорівнює груповій швидкості.

Прирівнюючи відповідні формули 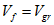і вирішуючи отримане рівняння, визначаємо значення хвильового числа стійкого стану: 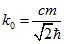(2.6). При цьому значення швидкості буде 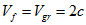. І відповідне значення кругової частоти отримаємо: 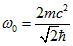(2.7). Таким чином, ми отримали сферичну хвилю без дисперсії. Так як, за умови рівності фазової і групової швидкостей, дисперсія зникає.

Отримане значення швидкості в два рази вище швидкості світла. Але це не швидкість руху електрона. Так як ми розглядаємо електрон в нерухомому стані. Це швидкість поширення в просторі сферичної хвилі де Бройля (для початкової версії гіпотези), тобто хвилі матерії. І оскільки отримана хвиля матерії поки що має невідому природу, то поки не будемо обмежувати її характеристики і зокрема швидкість поширення.

Перш ніж продовжити, звернемо увагу на таку обставину. Визначимо енергію спокою електрона відповідно до формули 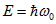. тоді отримаємо 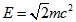. Як можна помітити, отримане значення енергії, в 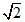рази більше очікуваного значення, енергії спокою електрона .

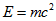Для усунення отриманого невідповідності, введемо поняття затравочной маси електрона. Яка вступаючи у внутрішні хвильові процеси, утворює енергію спокою 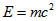. З цих міркувань отримаємо значення затравочной маси 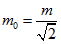. І в подальших розрахунках замість маси електрона будемо застосовувати затравочную масу.

Тоді остаточно отримаємо для стійкого стану значення хвильового числа 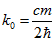(2.8) і значення кругової частоти 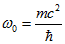(2.9).

Інтегруючи сферичні хвилі в невеликій околиці 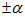стійкого стану (область 1 Рис.3.). Можна отримати сферичний хвильовий пакет без распливанія (2.10).

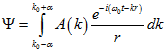(2.10)

Тепер, після отримання параметрів стійкого стану електрона, має сенс перейти до стаціонарного рівняння і остаточно отримати хвильову функцію голого нерухомого електрона.

Для цього, підставами отримане значення затравочной маси 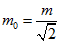і значення енергії спокою 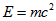в вихідне стаціонарне рівняння (1.1) без потенційної енергії. Тоді отримаємо: 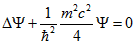(2.11)

Отримане рівняння, в теорії диференціальних рівнянь, відоме як рівняння Гельмгольца.

Рішення рівняння Гельмгольца

Для вирішення рівняння (2.11) можна застосувати стандартну методику розділення змінних в сферичної системі координат.

Уявімо хвильову функцію у вигляді твору радіальної і кутовий частин 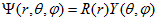(3.1)

Оператор Лапласа в сферичних координатах виглядає наступним чином: 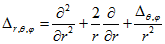(3.2) Підставимо твір (3.1) у вихідне рівняння (2.11).

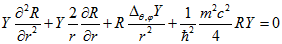Помножимо отримане рівняння на дріб .

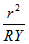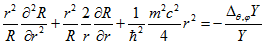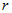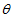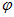(3.3) Як можна помітити ліва частина рівняння (3.3) залежить тільки від змінної , А права від змінних і . Отже, обидві частини рівні деякого постійного числа 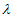. Що дозволяє відокремити радіальну частина рівняння від кутової частини.

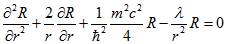(3.4) 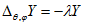(3.5) Далі представимо функцію 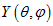у вигляді твору 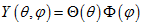(3.6). Кутова частина оператора Лапласа має наступний вигляд: 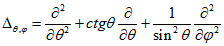(3.7). Підставами твір (3.6) в кутове рівняння (3.5) отримаємо: 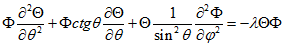(3.8).

Помноживши рівняння (3.8) на дріб 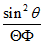отримаємо: 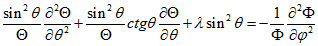(3.9) Ліва частина рівняння (3.9) залежить тільки від змінної 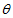а права частина тільки від змінної 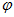. Отже, обидві частини рівні деякого постійного числа, яку позначимо 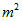. В результаті отримаємо два рівняння: 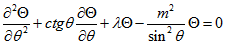(3.10) і 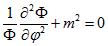(3.11)

Рішення 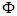рівняння (3.11) добре відомо 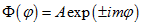(3.12). Так як при тотожних значеннях кута 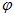( 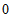і 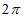) Функція повинна мати одне і те ж значення, то 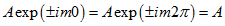і 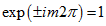. Використовуючи формулу Ейлера для комплексних чисел: 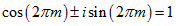, отримаємо 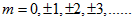Таким чином, 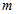може приймати тільки цілочисельні значення. Константа 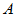знаходиться з умови нормування функції 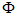. Але оскільки стандартна нормировка і імовірнісна інтерпретація хвильової функції тепер вже не діють, то поки це питання обговорювати не будемо.

Для вирішення 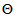рівняння (3.10), скористаємося математичним інтернет ресурсом WolframAlpha

Рішення дає: 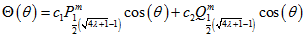(3.13)

Тобто, рішенням є, сума приєднаних функцій Лежандра першого і другого роду.

зробимо позначення 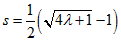(3.14). Мінлива 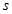у нас буде асоціюватися з квантовим числом спина. Визначимо область можливих значень квантового числа 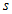. З формули (3.14) випливає, що 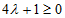отже 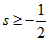(3.15). Переписавши залежність (3.14) щодо 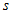отримаємо 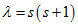(3.16) як і слід було очікувати. Таким чином кутова частина хвильової функції матиме вигляд:

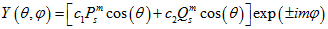(3.17)

Оскільки у нас електрон знаходиться в нерухомому стані, то звичайні умови квантування орбітального моменту не мають місця. Тому поки не можемо говорити, що квантове число 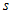може приймати тільки цілі або напівцілим значення. Область можливих значень 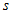буде обмежуватися тільки співвідношенням (3.15) і умовою нерозривності кутовий частини хвильової функції (3.17). Конкретні значення квантових чисел 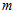і 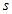і констант інтегрування 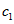і 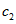залежатимуть від зовнішніх чинників. Тобто від граничних умов конкретного завдання. У роботах автора [5] наведено підхід, згідно з яким квантові числа 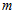і 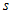можуть приймати як цілі так і напівцілим значення. Ми вважаємо цей підхід розумним.

Наведемо для наочності кілька графічних прикладів кутовий частини хвильової функції при різних значень квантових чисел 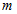і .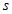

Перейдемо до вирішення радіального рівняння (3.4). Для цього скористаємося математичним інтернет ресурсом WolframAlpha

Перепишемо рівняння (3.4) з урахуванням позначення (3.16).

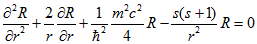(3.18)

Рішення має вигляд: 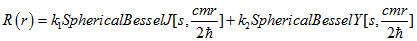(3.19)

Тобто є комбінацією сферичних функцій Бесселя першого і другого роду. Як відомо, сферична функція Бесселя другого роду необмежена при 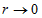. Тому приймаємо 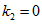. І остаточно радіальна частина хвильової функції матиме вигляд:

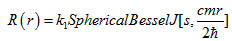(3.20)

Наведемо графік радіальної хвильової функції в атомних одиницях Хартрі, для перших кількох значень квантового числа 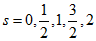. Оскільки питання нормування поки не обговорюємо, з наведених причин, то приймемо 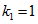. В одиницях Хартрі маса електрона 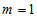, Постійна Планка 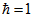і швидкість світла .

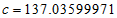Мал. 4. Графік радіальної частини хвильової функції при значеннях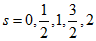

Таким чином, повна хвильова функція електрона представлятиме, твір радіальної, кутовий і залежить від часу частин.

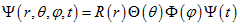
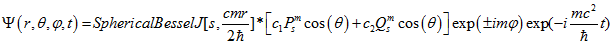(3.21)

Результати та обговорення

Як було показано, електрон має внутрішній хвильової процес з частотою 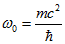. Хвильовий процес виходить в назовні і утворює хвилі матерії. При цьому хвильове число одно 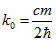, Отже довжина хвилі дорівнює 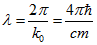, А швидкість поширення в просторі дворазово перевищує швидкість світла. Отже, хвилі матерії мають не електромагнітну природу.

Як відомо, електрон характеризується експериментально виявлених значенням: довжиною хвилі Комптона 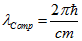. Отже, отримана довжина хвилі становить дворазову величину Комптонівське довжини хвилі 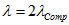. Звідси можна зробити припущення, що Комптонівська довжина хвилі пов'язана з хвильовими властивостями електрона.

Свого часу Е. Шредінгер не був згоден з чисто корпускулярним поясненням ефекту Комптона. І опублікував своє хвилеве опис [9].

"Шредінгер стверджував, що рентгенівське випромінювання може дифрагувати на стоячій" хвилі щільності заряду ", створеної падаючим і відбитим електроном, так само як світло дифрагує на стоячій хвилі ультразвуку (Born and Wolf 1959)."

Далі виявлено, що в коливальному процесі бере участь не вся маса електрона. В результаті, вводиться поняття затравочной маси 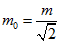. Тобто, маса електрона формується, в результаті вступу затравочной маси у внутрішній хвильової процес. За аналогією можна припустити, що і приманки маса теж утворюється в результаті хвильового процесу другого ступеня. І отже, матерія має багатоступеневу, вкладену один в одного хвильову структуру, як матрьошка.

Встановлено, що спін електрона не обов'язково повинен мати значення 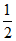. Область можливих значень квантових чисел електрона ще належить вивчати.

Отримані результати відкривають нові горизонти для теоретичних і експериментальних досліджень. Дозволяють по новому поглянути на багато експериментальні результати, в яких фігурують хвильові властивості електрона.

1. Луї де Бройль. Вибрані наукові праці. Т. 1. Становлення квантової фізики: роботи 1921 - 1934 років. - М .: Логос, 2010. - 556 с.
2. Gouan`ere, M. et al., Experimental observation compatible with the particle internal clock, Annales de la Fondation Louis de Broglie 30, 109-114 (2005)
3. A search for the de Broglie particle internal clock by means of electron channeling P.Catillon, N.Cue, MJGaillard, R.Genre, M.Gouanère, RGKirsch, JC.Poizat, J.Remillieux, L.Roussel and M.Spighel
4. Квантова теорія полів руху Д.В.Гламазда Уральський федеральний університет, Єкатеринбург 18 жовтня 2011 р
5. Холодова С.Є., Перегудін С.І. Спеціальні функції в задачах математичної фізики. - СПб: НДУ ІТМО, 2012. - 72 с.
6. On electron channeling and the de Broglie internal clock M. Bauer Instituto de F'ısica, niversidad Nacional Aut'onoma de M'exico and AP 20-364, 01000 M'exico, DF, MEXICO
7. Hunting for Snarks in Quantum Mechanics David Hestenesa Physics Department, Arizona State University, Tempe, Arizona 85287.
8. Srhrodinger E. The Compton effect. Annalen der Physik. 1927. V. 28. P. 257 - 264.

Кількість переглядів публікації: Please wait

Всі статті автора «Дангян Араік Еміль»