Дослідницька робота "Порівняння трикутників в геометрії Евкліда і в геометрії Лобачевського"
Муніципальне бюджетне загальноосвітній заклад
«Гімназія №2» г .Брянск
Методичне об'єднання математики, фізики та інформатики
ДОСЛІДНИЦЬКА РОБОТА
Порівняння трикутників в геометрії Евкліда і геометрії Лобачевського
виконала:
учениця 7 «Б» класу
МБОУ «Гімназія № 2»
Іваницька Аліна
Керівник роботи:
Новікова Т.М.
Г. Брянськ - 2016 р
ЗМІСТ
Введення ............................................................................................. 3
1.Історія досліджень трикутника як фігури і як поняття
Поняття «Геометрія» як науки і поняття «Трикутник» як геометричної фігури ...... .................................. ............................................. 4
Трикутники в древньому і сучасному світі ................................. ..4
2.Основні відомості про особливості геометрії Евкліда
2.1.Особенності в геометрії Евкліда ............................................. ... 7
2.2.Понятіе трикутник в Евклідовій геометрії .............................. .... 8
3.Основні відомості про особливості геометрії Лобачевського
3.1.Основние відмінності геометрії Лобачевського ................................. ... 9
3.2.Понятіе трикутник в геометрії Лобачевського .............................. 9
4.Проаналізіровать трикутник в геометрії Евкліда і Лобачевського ......... ..11
5.Заключеніе роботи ........................................................................... .14
ВСТУП
Мене зацікавила така на перший погляд проста фігура, як трикутник. Я вирішила дізнатися про трикутниках, які відрізняються від тих, що ми вивчаємо в шкільній програмі, тим самим вийти за курс підручника і знайти для себе і для однолітків інформацію, яка мало кому відома. Я вважаю, що це дуже важливо так як це розвиває мислення, кмітливість, винахідливість, розуміння простору навколо. Дослідницька робота дає зрозуміти, що є в цьому світі дуже багато того, що мені невідомо .Саме тому актуальність даної роботи дуже важлива для розвитку кожної людини.
Мета роботи: проаналізувати і порівняти «Трикутник» в геометрії Евкліда і в геометрії Лобачевського
Етапи роботи:
1. Вивчення теоретичної основи поняття «Трикутник» в природі, в науці і в практиці.
2. Вивчення особливостей геометрії Евкліда і Лобачевського.
3.Сопоставленіе поняття «Трикутник» в геометрії Евкліда і геометрії Лобачевського.
4.Ізготовленіе наочного електронного посібника за матеріалами дослідницької роботи.
5.Практіческое застосування практичних знань на заняттях факультативу.
6.Оформленіе роботи, презентації на конференцію.
Завдання роботи 1.История трикутника
2.Увідеть трикутники в навколишньому світі.
3.Ізучіть і проаналізувати особливості Евклідовій геометрії.
4.Ізучіть і проаналізувати геометрію Лобачевського
5.Сравніть поняття геометрії, властивості, ознаки, особливості трикутників в геометрії Евкліда і в геометрії Лобачевського.
6.Сопоставіть трикутники в Евклідовій геометрії і геометрії Лобачевського (таблиця)
7.Составіть фрагмент засідання за матеріалами роботи.
8. Підготувати електронний посібник для уроку геометрії за матеріалами роботи.
9.Сделать висновок
1.1.Геометрія виникла дуже давно, це одна з найдавніших наук. Геометрія (грецьке, від ge o - земля і metrein - вимірювати) - наука про простір, точніше - наука про форми, розміри і межі тих частин простору, які в ньому займають речові тіла. Важливу роль грали і естетичні потреби людей: бажання прикрасити своє житло і одяг, малювати картини навколишнього життя. Все це сприяло формуванню і накопиченню геометричних відомостей. За кілька століть до нашої ери в Вавилоні, Китаї, Єгипті та Греції вже існували початкові геометричні знання, які добувалися в основному дослідним шляхом, але вони не були ще систематизовані і передавалися від покоління до покоління у вигляді правил і рецептів, наприклад, правил перебування площ фігур, об'ємів тіл, побудова прямих кутів і т.д. Не було ще доказів цих правил, і їх виклад не представляло собою наукової теорії.
Трохи з історії…
Традиційно вважається, що родоначальниками геометрії є стародавні греки, що перейняли у єгиптян ремесло землемерия і вимірювання обсягів тіл, які перетворили його в науку.
Геометрична фігура, що складається з трьох точок, які не лежать на одній прямій і з'єднаних відрізками, називається трикутником.
1.2.Ізначально нашу увагу привернула звичайнісінька геометрична фігура-трикутник. Ми помітили, що трикутники оточують нас скрізь і всюди. Наприклад: дорожні знаки, гори, посуд, будівлі в архітектурі, іграшки, прикраси, лінійки і навіть чайні пакетики.
Ви коли-небудь помічали, що штатив варто також на трьох ніжках, а не на чотирьох? А чому? Три точки утворюють єдину площину, тому і штатив буде стояти стійкіше. І до речі, якщо подумки з'єднати ці три точки, то вийде трикутник.
У багатьох живописних роботах можна зустріти трикутники. Картина «Прихід весни і літа» художник-Бурлюк
Трикутні дахи також зустрічаються на кожній вулиці.
«Єгипетський трикутник»
Назва «єгипетський трикутник» з'явилося вже в 5 столітті до н.е. Належить воно прямокутного трикутника, сторони якого дорівнюють відповідно 3, 4 і 5.
Названий він був так тому, що дуже широко застосовувався ще в Стародавньому Єгипті в різних сферах життєдіяльності .Егіпетскій трикутник вже тоді був знайомий людям далеко за межами Стародавнього Єгипту, але, мабуть, його унікальні властивості помітили і почали використовувати вперше саме там.
В Єгипетському трикутнику в просторі досить складно відкласти прямий кут, (як же це зробити, коли в природі рідко зустрінеш прямі лінії, а вже тим більше прямі кути, немає від чого відштовхуватися, але єгиптяни винайшли цікавий спосіб. Вони брали мотузку, відміряли на ній вузликами 12 частин, а потім складали з неї трикутник, сторони якого рівні 3, 4 і 5 частин відповідно. В цьому трикутнику прямий кут виходив сам собою! а вже маючи такий інструмент, вони могли з великою точністю будувати свої споруди, наприклад, піраміди. А та ж використовувати його для розмітки землі під сільськогосподарські роботи.
Єгипетський трикутник тісно пов'язаний з Піфагором.
Можливо, вивчення цікавих особливостей єгипетського трикутника і підштовхнуло Піфагора на спробу узагальнення залежностей у всіх інших прямокутних трикутниках. Що йому, як відомо, вдалося!
До речі, виявляється, теорема Піфагора потрапила в Книгу Рекордів Гіннеса як теорема з найбільшою кількістю доказів (їх налічується близько 500)
Головна міра довжини - лікоть. Прямокутний трикутник був зі сторонами 3 ліктя, 4 ліктя і 5 ліктів.
Трикутник-містична фігура .Він оповитий безліччю історій, легенд і таємниць. Бермудський трикутник (англ. Bermuda Triangle) - район в Атлантичному океані, в якому відбуваються таємничі зникнення морських і повітряних суден. Район обмежений трикутником, вершинами якого є Флорида, Бермудські острови і Пуерто-Ріко. Тому сміливо можна сказати, що трикутник зустрічається і в географічній сфері.
На уроках географії ми, дізнаючись все більше і більше про горах, помітили, що вони схожі на трикутники, але сторони цих «трикутників» спотворені. Ми наочно порівняли їх і зрозуміли, що це що - то нове для нас.
Трикутники в природі
Коли ми обговорювали проект, то дивлячись у вікно ми помітили, що дерева мають форму трикутників, але не зовсім схожих на ті, що ми вивчали в шкільному курсі. Ми вирішили розібратися саме з цими «дивними» трикутниками.
Завдяки цій інформації, ми показали, що трикутники можна зустріти не тільки в підручниках, а й на дорогах, в містах, в живопису, в архітектурі і в багатьох інших сферах .Нас зацікавила ця фігура і ми вирішили дізнатися відмінність трикутників в просторі і на площині . З'ясувати в чому вони схожі, і як люди прийшли до іншої геометрії, до абсолютно іншим трикутниках
2.1..Евклід-давньогрецький вчений, що жив близько 300 г .до .н .е. У його тринадцяти книгах «Начала» вперше було представлено аксіоматична побудова геометрії. Протягом близько двох тисячоліть ця праця залишається основою систематичного курсу геометрії. Цар Птолемей запитав у Евкліда, чи не можна знайти більш короткий і менш виснажливий шлях до вивчення геометрії, ніж його «Начала». Евклід на це відповів: «У геометрії немає царського шляху»
Ім'я Евкліда назавжди пов'язане з одним з відгалужень математики, який отримав назву «Евклід геометрія». Настільки міцна слава закріпилася за Евклідом заслужено, завдяки його праці «Начала». У школах усього світу, довгі століття геометрія викладалася по «Початкам» Евкліда. В англійських школах до сьогоднішнього дня підручники геометрії за своєю формою нагадують цей учений трактат. У світовій літературі "Почала" належать до числа найпопулярніших і поширених математичних праць. Незважаючи на таку величезну популярність Евкліда як автора «Начал», сам він, його вигляд і життєвий шлях відомі дуже мало. Ні історично вірних відомостей про його життя, невідомі навіть точні дати його народження і смерті. Великі заслуги Евкліда. Про те, як високо оцінені його праці, свідчить факт, що "Почала" залишалися фундаментальним математичним працею протягом понад 2000 років.
Як відомо, в III столітті до нашої ери грецький геометр Евклід у своїй книзі "Початки" сформулював систему аксіом, з яких послідовно, одна за одною, виводяться всі основні теореми геометрії. І ніколи не виходило двох суперечать одна одній теорем, докази яких рівноправно випливали б з прийнятої системи аксіом. Це означає, що аксіоматика Евкліда несуперечлива.
Аксіоми геометрії Евкліда є продуктом повсякденних людських спостережень, крім однієї - аксіоми про паралельних, званої також п'ятим постулатом.
Першим систематичним викладом геометрії, що дійшли до нашого часу, є "Початки" - твори олександрійського математика Евкліда. В "Засадах" був розвинений аксіоматичний підхід до побудови геометрії, який полягає в тому, що спочатку формулюються основні положення (аксіоми), а потім на їх основі за допомогою міркувань доводяться інші твердження (теореми). Виклад геометрії Евкліда довгий час служило недосяжним зразком точності, бездоганності і строгості. Тільки на початку 20 століття математики змогли поліпшити логічні підстави геометрії.
Основні постулати Евкліда:
З кожної точки до всякої іншої точки можна провести пряму;
Кожну обмежену пряму можна продовжити невизначено;
З будь-якого центру можна описати коло будь-якого радіусу;
Всі прямі кути рівні;
Через точку що не лежить на даній прямій можна провести пряму, паралельну даній і тільки одну.
2.2На базі цих постулатів йшло успішний розвиток геометрії, але в той час як інші постулати вважалися абсолютно очевидними, очевидність п'ятого постулату оскаржувалася. Багато століть зусилля великої кількості вчених були спрямовані на доказ п'ятого постулату. Це пояснювалося тим, що число аксіом прагнули звести до мінімуму. Вчені думали, що п'ятий постулат можна довести як теорему, спираючись на інші. Багато геометри намагалися обійти його, замінюючи п'ятий постулат іншим, що здавався більш очевидним. На цьому шляху було сформульовано багато положень, але всі вони були еквівалентні п'ятого постулату Евкліда.
наприклад:
сума кутів трикутника дорівнює 180 °,
у всіх трикутниках сума кутів одна і та ж,
через будь-яку точку всередині кута можна провести січну, що перетинає обидві сторони кута,
існують два подібних, але не рівних трикутника,
теорема Піфагора,
для будь-якого трикутника існує описана окружність і ін.
Особливий інтерес математиків завжди викликала п'ята аксіома про паралельні прямі. На відміну від інших аксіом елементарної геометрії, аксіома паралельних не має властивість безпосередній очевидності. Тому на всьому протязі історії геометрії мали місце спроби довести аксіому паралельних, тобто вивести її з інших аксіом геометрії.
Саме геометрію Евкліда ми вивчаємо досі, але ми вирішили піти далі і дізналися про «інший» геометрії, яку відкрив Н. І. Лобачевський.
3.1.Ніколай Іванович Лобачевський-російський математик, творець неевклідової геометрії, діяч університетської освіти та народної освіти. Відомий англійський математик Вільям Кліффорд назвав Лобачевського «Коперником геометрії». Відкриття Лобачевського, яке не отримало визнання сучасників, вчинила переворот в уявлення про природу простору, в основі якої більше 2 тисяч років лежало вчення Евкліда, і справила величезний вплив на розвиток математичного мислення .Труди з алгебри, математичного аналізу, теорії ймовірностей, механіки, фізики та астрономії.
Діяльність Лобачевського викликає здивування. Поряд з великою адміністративної та педагогічною роботою він, не покладаючи рук, займався і наукою. Лобачевському було всього 34 роки, коли він вирішив «багатовікову» проблему V постулату з «Начал» Евкліда і побудував свою, неевклідову геометрію.
Ім'я Лобачевського відомо всьому світу. Він увійшов в історію математики як революціонер в науці і «Коперник геометрії». Микола Лобачевський вирішив проблему, над якою людство безплідно билося більше двох тисяч років. Аналізуючи спроби довести V постулат, Лобачевський зробив надзвичайно сміливий висновок про його недовідності. Раз V постулат недоказуем як теорема, то принципово можлива інша геометрія, відмінна від евклідової, - неевклідова геометрія, відправною точкою якої є заперечення V постулату.
3.2. «Геометрія Лобачевського», як її тепер називають, є найбільшим завоюванням науки і становить цілу епоху в розвитку математики і суміжних їй наук.
Лобачевський, отримавши в геометрії незвичайні результати, натрапив на відсталість і рутину. Вченої висміяли як людини, навіженого в науці, який написав сатиру на геометрію, намагаючись довести, що біле - це чорне, кругле - чотирикутне, що сума всіх кутів в прямолінійному трикутнику менше двох прямих і ряд інших дурниць .Пріходітся дивуватися мужності Лобачевського, який без моральної підтримки з боку, оточений непроникною стіною байдужості, не занепав духом і проніс свої переконання через всю многотрудною життя.
Геометрія Лобачевського має обширні вживання як в математиці, так і в фізиці. Історичне її значення полягає в тому, що її побудовою Лобачевський показав можливість геометрії, відмінної від евклідової, що знаменувало нову епоху в розвитку геометрії і математики взагалі. Відкриття неевклідової геометрії зробило переворот не тільки в геометрії.
Лобачевський залишився вірним науці навіть тоді, коли на нього обрушилося відразу кілька негараздів (смерть старшого сина, погіршення матеріального становища, насильницьке
відсторонення від університету). За рік до смерті, будучи абсолютно сліпим, Лобачевський диктує своїм учням новий твір, назване їм «Пангеометрія», де показує, що евклідова геометрія є окремим випадком неевклідової геометрії. Цю останню свою роботу він з любов'ю присвячує Казанського університету, де пройшло все його творче життя Геометрія Лобачевського має обширні вживання як в математиці, так і в фізиці. Історичне її значення полягає в тому, що її побудовою Лобачевський показав можливість геометрії, відмінної від евклідової, що знаменувало нову епоху в розвитку геометрії і математики взагалі. Відкриття неевклідової геометрії зробило переворот не тільки в геометрії і навіть не тільки в математиці, але можна сказати, в розвитку людського мислення взагалі.
24 лютого 1856 року Лобачевського не стало. Якого-небудь десятка років не дожив він до загального визнання своїх людей.
Розвитку і поширенню ідей Лобачевського сприяли своїми працями такі чудові вчені, як: Герман Людвіг, Карл Гаусс, Фердинанд Гельмгольц, Бернхард Ріман, Анрі Пуанкаре.
4. «Чим відрізняється геометрія Лобачевського
від геометрії Евкліда? »
Евклидова аксіома про паралельних прямих: через точку, що не лежить на даній прямій, проходить тільки одна пряма, що лежить з даною прямою в одній площині і не перетинають її.
Аксіома Лобачевського про паралельні прямі: через точку, що не лежить на даній прямій, проходять принаймні дві прямі, що лежать з даною прямою в одній площині і не перетинають її.
Висновок: геометрія Лобачевського відрізняється від евклідової лише в одній аксіомі - п'ятою. Але головна відмінність криється в розумінні самої природи простору.
подібні трикутники
1 ознака: Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого трикутника, то трикутники подібні.
2 ознака: Якщо кут одного трикутника дорівнює куту другого трикутника, а сторони, що утворюють цей кут в одному трикутнику, пропорційні відповідним сторонам іншого, то такі трикутники подібні.
3 ознака: Якщо три сторони одного трикутника відповідно пропорційні трьом сторонам іншого, то такі трикутники подібні.
В геометрії Лобачевського не існує подібних трикутників
Різниця в ознаках рівності трикутників
геометрія Евкліда
У Геометрії Евкліда існує всього 3 ознаки рівності трикутників
В геометрії Лобачевського
В геометрії Лобачевського має місце четвертий ознака рівності трикутників: якщо кути одного трикутника відповідно рівні кутах іншого трикутника, то ці трикутники рівні.
Сума кутів трикутника
геометрія Евкліда
Як, наприклад, в геометрії Евкліда доводиться, що сума кутів трикутника дорівнює 180 °? Класичне доказ приведено на малюнку. Використовується властивість кутів при навхрест лежачих прямих, і виходить, що сума внутрішніх кутів трикутника дорівнює 180 °
геометрія Лобачевського
Так як в геометрії Лобачевського паралельність зберігається тільки в одному напрямку, то для знаходження суми кутів трикутника потрібно провести дві прямі, паралельні даній, в різні боки. Зрозуміло, що тепер сума кутів трикутника менше 180. Ця різниця була названа Лобачевским дефектом трикутника.
Сума кутів трикутника
Теорема про суму кутів трикутника - класична теорема геометрії Евкліда. Стверджує, що сума кутів трикутника на евклідової площини дорівнює 180 °.
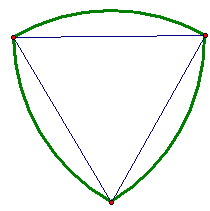
Визначимо криволінійний трикутник як фігуру, що складається з трьох точок, які не лежать на одній прямій і трьох один кіл, що сполучають ці точки. Наприклад, правильний вигнутий трикутник можна отримати наступним способом. З кожної вершини правильного трикутника проведемо окружність, радіус якої дорівнює його стороні, і найменшою з двох можливих дуг цієї окружності з'єднаємо сусідні вершини. Справа в тому, що розглядаючи суму кутів трикутника ми дізналися дивовижні факти:
На сфері сума кутів трикутника завжди перевищує 180 °
У площині Лобачевського сума кутів трикутника завжди менше 180 °
Геометрія Евкліда і геометрія Лобачевського
1) Геометрія на площині
2) Існують ознаки подібних трикутників
3) 3 ознаки рівності трикутників
4) Сума кутів трикутника завжди дорівнює 180 °
геометрія Лобачевського
1) Геометрія в просторі
2) Подібних трикутників не існує
3) 4 ознаки рівності трикутників
4) Сума кутів трикутника менше 180 °, а на сфері больше180 °
5. Висновок роботи
1.Геометрія Евкліда працює на маленькій поверхні, а геометрія Лобачевського на розгорнутій площині з урахуванням кривизни поверхні.
2. Трикутники геометрії Евкліда ми зустрічаємо в підручниках, в науках, а трикутники Лобачевського ми можемо побачити в навколишньому світі.
3.Геометрія Лобачевського (в тому числі і 5-ий постулат) абсолютно вірна, якщо її розглядати не на площині, а на поверхні гіперболічного параболоїда (увігнутою поверхні, що нагадує сідло).
4.Любая теорія сучасної науки вважається єдино вірною, поки не створена наступна. Це своєрідна Аксіома розвитку науки.
Висновок дослідницької роботи
Дана дослідницька роботи мене зацікавила. В ході роботи, я дізналася історичні відомості про математику і вчених, що розвивали математику, подивилася на трикутники, як у повсякденному житті, так і з наукової точки зору, освоїла нові програми в комп'ютері .Не варто забувати, що в роботі важливо все: від вибору шрифту і фону в презентації до складання плану роботи, пошуку інформації. Швидше за все, в наступному році я також проведу дослідницьку роботу або складу проект, адже дуже важливо кожній людині розвивати себе, дізнаватися нову інформацію, нові дивовижні факти.
Список використаних джерел:
https://ru.wikipedia.org/wiki/Евклид
https://ru.wikipedia.org/wiki/Геометрия_Лобачевского
https://ru.wikipedia.org/wiki/Лобачевский,_Николай_Иванович
http://pandia.ru/text/79/014/74072.php
http://xreferat.com/54/1282-1-evklid-i-lobachevskiiy.html
http://schools.keldysh.ru/sch1215/data/t_geom3.html
http://to-name.ru/biography/nikolaj-lobachevskij.htm
http://sto-geniev.narod.ru/uchenye/lobachevskiy.html
https://ru.wikipedia.org/wiki/Треугольник
http://www.chitalnya.ru/work/198440/
http://dic.academic.ru/dic.nsf/bse/104199/Лобачевского
http://www.bestreferat.ru/referat-207255.html
http://pandia.ru/text/79/014/74072.php
Ви коли-небудь помічали, що штатив варто також на трьох ніжках, а не на чотирьох?А чому?