Реферат на тему "Геометрія Лобачевського"

державне бюджетне професійний освітній заклад

Ростовської області

«Волгодонский педагогічний коледж»

(ГБПОУ РО «ВПК»)

реферат

на тему

«Геометрія Лобачевського Н.І.»

Виконав: студентка ПНК-2 Морковский Е.С.

Перевірив: викладач Молотова Н.Є.

Волгодонськ

2017р

ЗМІСТ

1 Введення .................................... .. .................................. ... ..3стр.

2 Геометрія Лобачевського ................................. .. ............... .. ... .3-7стр.

3 Доказ незалежності 5 постулату ................................. 7-9стр.

4 Геометрія Лобачевського в реальному світі ........................ ... ...... .9-10стр.

5 Приклади поверхонь Лобачевського ........................... ... ....... 11-12стр.

6 Висновок ........................................................................ 12стор.

7 Список літератури ............................................................... .13стр.

ВСТУП

У площині через точку, що не лежить на даній прямій, можна провести одну і тільки одну пряму, паралельну даній.

Ця аксіома вірна тільки для геометрії Евкліда в просторі, яке теж називається Евклідовому. Існують інші геометрії та інші простору, де ця аксіома не виконується. Одну з таких геометрій придумав наш співвітчизник Микола Іванович Лобачевський.

Мета цього реферата- знайомство з геометрією Лобачевського, вивчення аксіоматичного підходу в побудові будь-якої теорії, систематизація отриманих знань, вивчення докази п'ятого постулату, розгляд локальних поверхонь з постійною негативною кривизною, на яких вірна геометрія Лобачевського

Геометрія Лобачевського допомагає зовсім по-іншому поглянути на навколишній світ. Щоб її зрозуміти, необхідно володіти фантазією і просторовою уявою.

Спочатку геометрія Лобачевського вважалася непридатною до практичного застосування, так як простір, в якому ми живемо, не відповідає простору, описуваного цієї геометрією. Однак закони, виведені Лобачевским, незабаром знайшли практичне застосування.

ГЕОМЕТРІЯ ЛОБАЧЕВСКОГО

Розглянемо основні поняття, на яких базується виклад геометрії Лобачевського. За основні об'єкти прийняті точка, пряма і відрізок. За основні відносини між цими об'єктами приймаються:

Точка належить фігурі, зокрема прямий;

Точка лежить між двома точками для точок прямої.

Відрізком називається частина прямої, яка складається з усіх точок цієї прямої, що лежать між двома даними її точками. Ці точки називаються кінцями відрізка.

Променем AB називається частина прямої, що складається з усіх її точок, що лежать по ту ж сторону від точки А, що і точка В. точка А називається вершиною променя.

Кутом називається фігура, яка складається з точки - вершини кута і двох різних променів, що виходять з цієї точки, - сторін кута.

Аксіоматика Лобачевського відрізняється від аксіоматики планіметрії Евкліда лише однієї аксіомою: аксіома паралельності замінюється на її заперечення - аксіому паралельності Лобачевського.

Уявною геометрією Лобачевський назвав її тому, що вона поки залишалася доступною лише уяві, а не досвіду.

Якщо замість V постулату допустити, що для пари «точка-пряма» V постулат хибний, то отримана система аксіом буде описувати геометрію Лобачевського. Зрозуміло, що в геометрії Лобачевського все еквівалентні V постулату Евкліда затвердження невірні.

На площині через точку, що не лежить на даній прямій, проходить не менше двох прямих, не яка перетинає дану (рисунок 3).

малюнок 3 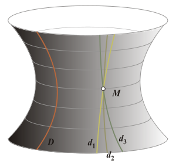Наочне уявлення геометрії Лобачевського: через точку M

проходять дві прямі, паралельні прямій D.

Паралельні і суперечать прямі

Лобачевський змінив саме розуміння паралельних ліній. У Евкліда непересічні і паралельні - одне і те ж, у Лобачевського: з усіх, що не перетинають дану пряму АВ, лише дві прямі називаються паралельними, при цьому розрізняють напрямок паралельності.

Паралельність прямих на евклідової площини можна характеризувати і іншими властивостями, наприклад, наявністю у них багатьох спільних перпендикулярів або постійністю довжин цих перпендикулярів.

На площині Лобачевського для двох непересічних прямих ці твердження невірні. Тут можливі два випадки: прямі мають загальний перпендикуляр і прямі не мають загального перпендикуляра

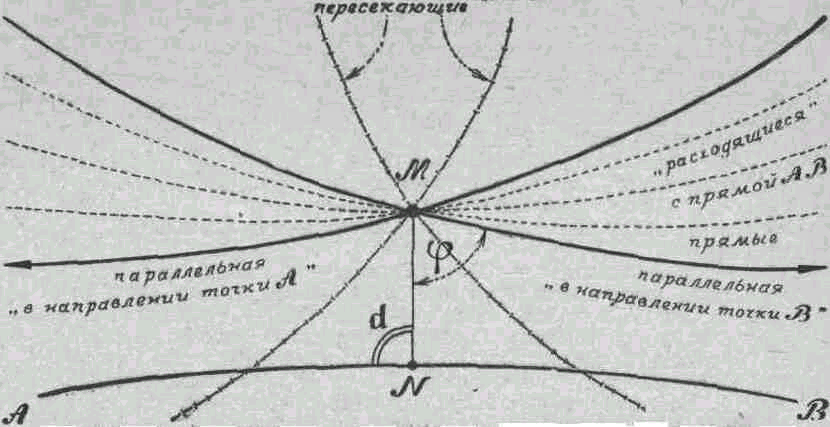
малюнок 4

Тому постулат уточнюється: якщо дана пряма АВ і не лежить на ній точка М, то через точку М в площині МАВ можна провести дві прямі, паралельні даній прямій АВ. Паралельними Лобачевський, отже, називає такі, які відокремлюють непересічних від перетинають дану пряму АВ. Відстань між прямою АВ і кожної з паралельних не залишається постійним - зменшується в сторону паралелізму і збільшується в протилежну сторону. Паралельні прямі можуть близько підійти один до одного, але вони не можуть перетнутися.

Площина, в якій існують такі паралельні, прийнято називати площиною Лобачевського. Ця площина зовсім не «плоска» в Евклідовому сенсі. В евклідовій площині кут паралельності незмінний і завжди дорівнює 90 °; в геометрії Лобачевського він може приймати всі значення - від 0 до 90 °. Отже, евклідова геометрія є приватний (граничний) випадок геометрії Лобачевського, в якій кут паралельності змінний. Геометрично величина кута паралельності залежить від довжини перпендикуляра MN; тобто якщо перпендикуляр зменшується, кут паралельності збільшується, поступово наближаючись до 90 °.

Таким чином, в новій геометрії існує взаємозалежність величини кута і довжини відрізка. Для точки М, що знаходиться від заданої прямої на відстані MN = a (рис. 4), Лобачевський визначив формулу для кута паралельності φ = П (a):

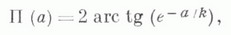
де k - постійна, що визначає фіксований за величиною відрізок. Вона отримала назву радіусу кривизни простору Лобачевського. Подібно сферичної геометрії існує безліч просторів Лобачевського, що розрізняються величиною k.

Ця залежність називається функцією Лобачевського. Величина константи k залежить від конкретних фізичних умов в даній частині світового простору. Виключно велика величина константи свідчить про те, що наш простір має величезний радіусом кривизни і, отже, досить малої, близькою до нуля, кривизною, тобто простір в нашій частині всесвіту має плоский, евклидов характер.

В геометрії Лобачевського зберігаються всі теореми, які в геометрії Евкліда можна довести без використання п'ятого постулату. Наприклад, вертикальні кути рівні; кути при основі рівнобедреного трикутника рівні; з цієї точки можна опустити на дану пряму тільки один перпендикуляр і ін. Однак теореми, де застосовується аксіома паралельності, видозмінюються.

Наведемо (в сучасних позначеннях) кілька фактів геометрії Лобачевського, що відрізняють її від геометрії Евкліда і встановлених самим Лобачевським.

Теорема про суму кутів трикутника: У геометрії Лобачевського сума кутів будь-якого трикутника менше 180 °. Різниця між 180 ° і сумою кутів трикутника позитивна і називається дефектом (D) цього трикутника. Формула для площі трикутника S = k * D, тобто площа пов'язана з його дефектом. Найбільшу площу має трикутник з нульовими кутами, а його сторони мають нескінченну довжину (малюнок 5).

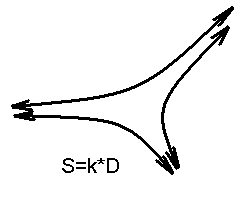
малюнок 5

• Два нерівних рівносторонніх трикутника мають нерівні кути.

• В геометрії Лобачевського не існує подібних фігур.

• Якщо кути одного трикутника дорівнюють відповідно кутам іншого трикутника, то ці трикутники рівні.

• Геометричне місце точок, що знаходяться на даному відстані від даної прямої і лежать по одну сторону є крива лінія, яка називається еквідістантой.

• Через точку, що не лежить на даній прямій проходить нескінченно багато прямих, які не перетинаються з даною, серед них дві паралельні прямі в сенсі Лобачевського, при цьому ми повинні відрізняти ще сторону паралельності

• Якщо прямі мають загальний перпендикуляр, то вони розходяться

• В геометрії Лобачевського існує залежність між кутами і довжиною сторін трикутника.

• Довжина кола не пропорційно її радіусу, а зростає швидше.

Можливі розташування двох прямих на площині Лобачевського: дві неспівпадаючі прямі або перетинаються в одній точці, або паралельні, або є розбіжними (рис 6).

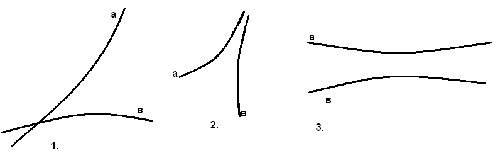
малюнок 6

На закінчення відзначимо, що Лобачевський з вичерпною повнотою розвинув всі розділи своєї неевклідової геометрії, включаючи тригонометрію і почала аналітичної та диференціальної геометрії.

Доказ НЕЗАЛЕЖНОСТІ п'ятого постулату

(побудова моделей)

Довести несуперечність нової геометрії ні Лобачевський, ні Бойяи не зуміли - тоді математика ще не мала у своєму розпорядженні необхідними для цього засобами. Тільки через 40 років з'явилися дослідження Е. Бельтрамі (1868), модель Клейна (1871) і модель Пуанкаре (1882), що реалізують аксіоматику геометрії Лобачевського на базі геометрії Евкліда.

У 1871 році Клейн запропонував першу повноцінну модель площині Лобачевського.

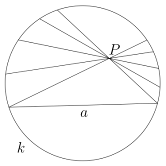
Площиною служить внутрішність круга, прямий - хорда кола без решт, а точкою - точка всередині кола. «Рухом» назвемо будь-яке перетворення круга в самого себе, яке переводить хорди в хорди. Відповідно, рівними називаються фігури усередині круга, переводяться одна в іншу такими перетвореннями. Тоді виявляється, що будь-який геометричний факт, описаний на такому мові, представляє теорему або аксіому геометрії Лобачевського. Іншими словами, будь-яке твердження геометрії Лобачевського на площині є не що інше, як твердження евклідової геометрії, що відноситься до фігур усередині круга, лише переказане в зазначених термінах. Евклидова аксіома про паралельних тут явно не виконується, так як через точку P, що не лежить на даній хорді а (тобто «прямій»), проходить скільки завгодно що не перетинають її хорд ( «прямих») (наприклад, b, b ').

Пізніше Пуанкаре, в зв'язку з завданнями теорії функцій комплексного змінного дав іншу модель. За площину Лобачевського приймається внутрішність круга, прямими вважаються дуги кіл, перпендикулярних колу даного круга, і його діаметри, рухами - перетворення, одержувані комбінаціями інверсій щодо кіл, дуги яких служать прямими.

Модель Пуанкаре чудова тим, що в ній кути зображаються звичайними кутами.

Межа кіл нескінченно зростаючого радіусу не їсти пряма, а особлива крива, звана граничної окружністю, або орициклом.

Межа сфер нескінченно зростаючого радіусу не їсти площину, а особлива поверхня - гранична сфера, або орисфере; чудово, що на ній має місце евклідова геометрія. Це служило Лобачевському основою для виведення формул тригонометрії.

Довжина кола не пропорційно радіусу, а зростає швидше.

Чим менше область в просторі або на площині Лобачевського, тим менше геометричні співвідношення в цій області відрізняються від співвідношень евклідової геометрії. Можна сказати, що в нескінченно малої області має місце евклідова геометрія.

У 1868 році італійський математик Е. Бельтрамі досліджував поверхню c постійною негативною кривизною, звану псевдосферу і довів, що на цій поверхні діє геометрія Лобачевського.

П

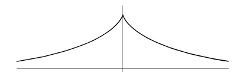трактриса

севдосфера (рис 7) - поверхня, утворена обертанням трактриса близько її асимптоти. Назва підкреслює схожість і відмінність із сферою, яка є прикладом поверхні з кривизною, також постійної, але позитивної.

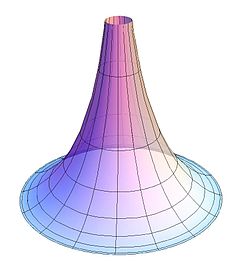
Малюнок 7 - Псевдосфера

Однак тут дається інтерпретація геометрії тільки локально, тобто на шматку, а не на всій площині Лобачевського.

ГЕОМЕТРІЯ ЛОБАЧЕВСКОГО В РЕАЛЬНОМУ СВІТІ

Якщо геометрія Евкліда є лише частиною геометрії Лобачевського, то виходить, що наш світ - не мир Евкліда. Чому ж ми не помічаємо різниці. Розглянемо таке поняття як гауссова кривизна простору. Якщо ми візьмемо криву поверхню, проведемо до якоїсь точки дотичну, проведемо в точку дотику відрізок, перпендикулярний дотичній площині, то ми отримаємо нормаль. Провівши через нормаль площину, ми можемо знайти окружність, найбільш щільно прилягає до поверхні. Так як ми можемо провести скільки завгодно площин, то ми можемо знайти окружності з мінімальним і максимальним радіусами. Використовуючи певні співвідношення, можна визначити кривизну простору, яка може бути як позитивна, так і негативна. На поверхнях з негативною кривизною і працює геометрія Лобачевського. Саме таку кривизну мають графіки інтенсивності всіх електромагнітних полів. Стан поверхні плазми також описується геометрією Лобачевського.

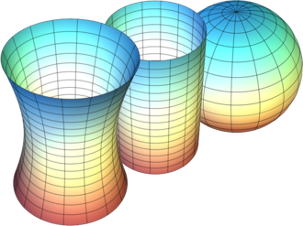
Малюнок 9 - Поверхности з негативною (зліва), нульовий (в центрі) і позитивної (праворуч) кривизною

Сам Лобачевський застосував свою геометрію до обчислення певних інтегралів.

Геометрія Лобачевського знаходить застосування також в теорії чисел, в її геометричних методах, об'єднаних під назвою «геометрія чисел».

Була встановлена ​​тісний зв'язок геометрії Лобачевського з кінематикою спеціальної (приватної) теорії відносності. Цей зв'язок заснована на тому, що рівність, що виражає закон поширення світла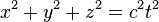

при розподілі на 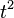, Тобто для швидкості світла, дає

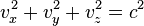
- рівняння сфери в просторі з координатами 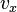, , 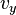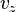- складовими швидкості по осях х, у, z (у «просторі швидкостей»). Отже, відповідно до моделі Клейна, в просторі швидкостей усередині сфери радіусу з, тобто для швидкостей, менших швидкості світла, має місце геометрія Лобачевського.

Чудове додаток геометрія Лобачевського знайшла в загальної теорії відносності . Якщо вважати розподіл мас матерії у Всесвіті рівномірним (це наближення в космічних масштабах допустимо), то виявляється можливим, що при певних умовах простір має геометрію Лобачевського. Таким чином, припущення Лобачевського про його геометрії як можливої ​​теорії реального простору виправдалося.

Значення геометрії Лобачевського для космології було виявлено А. А. Фрідманом. У 1922 році він знайшов рішення рівняння Ейнштейна, з якого випливало, що Всесвіт розширюється з плином часу. Метрика, знайдена А. А. Фрідманом, дає при фіксованому часу простір Лобачевського. Простір швидкостей спеціальної теорії відносності є простором Лобачевського. Геометрія Лобачевського з успіхом використовується при вивченні зіткнень елементарних частинок і при розробці ін. Питань ядерних досліджень.

Створення геометрії Лобачевського стало важливим етапом у розвитку вчення про можливі властивості простору. Особливе значення це мало для підстав математики, т. К. Принципи сучасного аксіоматичного методу вироблялися в значній мірі завдяки появі геометрії Лобачевського

Через деякий час ідеї Лобачевського були прийняті математиками, і наступним етапом розвитку геометрії стала еліптична геометрія Рімана. Ріман виходив з того, що через точку, що не лежить на даній прямій, взагалі не можна провести пряму, що не перетинає дану.

В геометрії Рімана:

• дві прямі завжди перетинаються, паралельні прямі зовсім немає;

• сума кутів прямолінійного трикутника більше 180 °;

• пряма має кінцеву довжину, площина - кінцеву площу та ін.

Окремим випадком еліптичної геометрії Рімана є сферична геометрія Рімана або геометрія не сфері.

Приклади ПОВЕРХОНЬ ЛОБАЧЕВСКОГО

Для поверхні Лобачевського необхідна постійна негативна кривизна в усіх її точках. Відомо безліч різних варіантів таких поверхонь:

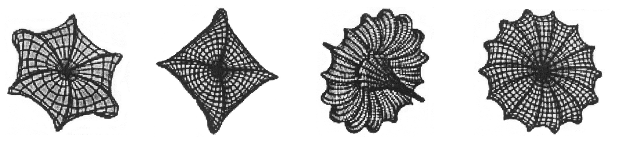Малюнок 10 - Псевдосферіческіе поверхні

У літературі описані різноманітні псевдосферіческіе поверхні обертання:

Малюнок 11- Псевдосферіческіе поверхні обертання

Багато поверхні постійної негативної кривизни названі іменами математиків, які їх досліджували і описали:

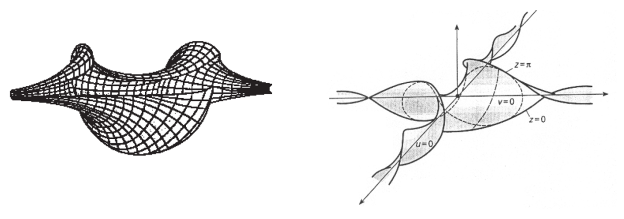Рісуно12 Поверхня Діні (зліва) і поверхня Біанкі - Амслера (праворуч)

На наведених малюнках видно, що поверхні постійної негативної кривизни або мають край, або замкнуті.

Кривизна простору проявляється в великих масштабах і поблизу масивних космічних тіл, а в повсякденному житті на нашій планеті ми можемо з успіхом користуватися геометрією Евкліда з великою точністю, так як нелінійні поправки на кривизну простору мізерно малі.

ВИСНОВОК

Хоча Лобачевський довів, що геометрія Евкліда не є єдино можливою, однак це не підірвало непорушність геометрії Евкліда.

В основі геометрії Евкліда лежать поняття і аксіоми, які пов'язані з діяльністю людини, з людською практикою. Тільки практика може вирішити питання про те, яка геометрія вірніше викладає властивості фізичного простору. Відкриття неевклідової геометрії дало вирішальний поштовх розвитку науки, сприяло більш глибокому розумінню навколишнього нас матеріального світу.

Вчених давно хвилювало питання - в якому світі ми живемо? Який геометрією він описується? Зараз Всесвіт розширюється, але якщо маса речовини цілому світові перевищить певний поріг, то розширення зміниться стисканням, тобто простір буде викривлений таким чином, що промінь світла, одного разу покинувши одну точку, повернеться назад, а це значить, ми живемо в світі еліптичної геометрії Рімана . Якщо маси не вистачить, то всесвіт буде розширюватися необмежено, а значить, ми живемо в світі гіперболічної геометрії Лобачевського

СПИСОК ЛІТЕРАТУРИ

Н.І. Лобачевський Полное собрание сочинений, тому перший, Геометричні дослідження з теорії паралельних ліній. Про початки геометрії, під ред. В.Ф.Каган, 1946.

Колесніков М. Лобачевський. Серія «Життя видатних людей». - М .: Молода гвардія, 1965

Широков П.А. Короткий нарис основ геометрії Лобачевського. /. - М .: Наука, 1983.

Бобров С.П. Чарівний дворога. /. М., Дитяча література., 1967.

За матеріалами сайту http://ru.wikipedia.org