Лобачевського геометрія
Лобач е вского геом е трия, геометрична теорія, заснована на тих же основних посилках, що і звичайна евклідова геометрія , За винятком аксіоми про паралельних, яка замінюється на аксіому про паралельні Лобачевського. Евклидова аксіома про паралельних свідчить: через точку, що не лежить на даній прямій, проходить тільки одна пряма, що лежить з даною прямою в одній площині і не перетинає її. У Л. р замість неї приймається наступна аксіома: через точку, що не лежить на даній прямій, проходять принаймні дві прямі, що лежать з даною прямою в одній площині і не перетинають її. Здавалося б, ця аксіома суперечить надзвичайно звичним уявленням. Проте як ця аксіома, так і вся Л. р має цілком реальний сенс (про що див. Нижче). Л. р була створена і розвинена Н. І. Лобачевским , Який вперше повідомив про неї в 1826. Л. р називається неевклідової геометрією, хоча зазвичай терміну «неевклидова геометрія» надають більш широкий зміст, включаючи сюди і ін. Теорії, що виникли слідом за Л. р і також засновані на зміні основних посилок евклідової геометрії. Л. р називається спеціально гіперболічної неевклідової геометрією (в протилежність еліптичній геометрії Рімана) (див. Неевклідові геометрії , Рімана геометрія ).
Л. р представляє теорію, багату вмістом і що має застосування як в математиці, так і в фізиці. Історичне її значення полягає в тому, що її побудовою Лобачевський показав можливість геометрії, відмінної від евклідової, що знаменувало нову епоху в розвитку геометрії і математики взагалі (див. геометрія ). З сучасної точки зору можна дати, наприклад, наступне визначення Л. р на площині: вона є не що інше, як геометрія усередині круга на звичайній (евклідової) площині, лише виражена особливим чином. Саме, будемо розглядати коло на звичайній площині (рис. 1) і внутрішність його, т. Е. Коло, за винятком обмежує його окружності, назвемо «площиною». Точкою «площині» буде точка всередині кола. «Прямий» будемо називати будь-яку хорду (наприклад, а, b, b ', MN) (з виключеними кінцями, т. К. Окружність кола виключена з «площині»). «Рухом» назвемо будь-яке перетворення круга самого в себе, яке переводить хорди в хорди. Відповідно, рівними називаються фігури усередині круга, переводяться одна в іншу такими перетвореннями. Тоді виявляється, що будь-який геометричний факт, описаний на такому мові, представляє теорему або аксіому Л. р Іншими словами, будь-яке твердження Л. р на площині є не що інше, як твердження евклідової геометрії, що відноситься до фігур усередині круга, лише переказане в зазначених термінах. Евклидова аксіома про паралельних тут явно не виконується, т. К. Через точку О, що не лежить на даній хорді а (т. Е. «Прямий»), проходить скільки завгодно що не перетинають її хорд ( «прямих») (наприклад, b, b '). Аналогічно, Л. р в просторі може бути визначена як геометрія усередині кулі, виражена у відповідних термінах ( «прямі» - хорди, «площині» - плоскі перетину нутрощі кулі, «рівні» фігури - ті, які переводяться одна в іншу перетвореннями, переводять кулю сам в себе і хорди в хорди). Таким чином, Л. р має абсолютно реальний сенс і настільки ж несуперечлива, як геометрія Евкліда. Опис одних і тих же фактів в різних термінах або, навпаки, опис різних фактів в одних і тих же термінах представляє характерну рису математики. Вона ясно виступає, наприклад, коли одна і та ж лінія задається в різних координатах різними рівняннями або, навпаки, один і той же рівняння в різних координатах представляє різні лінії.
Виникнення геометрії Лобачевського. Джерелом Л. р послужив питання про аксіому про паралельних, яка відома також як V постулат Евкліда (під цим номером твердження, еквівалентне наведеної вище аксіомі про паралельних, фігурує в списку постулатів в «Початки» Евкліда ). Цей постулат, зважаючи на його складність в порівнянні з іншими, викликав спроби дати його доказ на підставі інших постулатів.
Ось неповний перелік вчених, що займалися доказом V постулату до 19 в .: давньогрецький математики Птолемей (2 ст.), Прокл (5 ст.) (Доказ Прокла засноване на припущенні про кінцівки відстані між двома паралельними), Ібн аль-Хайсам з Іраку ( кінець 10 - початок 11 ст.) (Ібн аль-Хайсам намагався довести V постулат, виходячи з припущення, що кінець рухомого перпендикуляра до прямої описує пряму лінію), таджицький математик Омар Хайям (2-я половина 11 - початок 12 ст.), азербайджанський математик Насиреддін туями (13 ст.) (Хайям і Насир еддін при доказі V постулату виходили з припущення, що дві сходяться прямі не можуть при продовженні стати розбіжними без перетину), німецький математик К. Клавий (Шлюсселя, 1574), італійські математики П. Катальді (вперше в 1603 надрукував роботу, цілком присвячену питанню про паралельних), Дж. Бореллі (1658), Дж. Вітале (1680), англійський математик Дж. Валліс (+1663, опубліковано в 1693) (Валліс засновує доказ V постулату на припущенні, що для будь-якої фігури існує їй подібна, але не рівна фігура ). Докази перерахованих вище геометрів зводилися до заміни V постулату ін. Припущенням, що здавався більш очевидним. Італійський математик Дж. Саккери (1 733) зробив спробу довести V постулат від протилежного. Прийнявши пропозицію, що суперечить постулату Евкліда, Саккери розвинув з нього досить великі слідства. Помилково визнавши деякі з цих наслідків приводять до суперечностей, Саккери зробив висновок, що постулат Евкліда доведений. Німецький математик І. Ламберт (близько 1766, опубліковано в 1786) зробив аналогічні дослідження, однак він не повторив помилки Саккери, а визнав своє безсилля виявити в побудованій ним системі логічне протиріччя. Спроби докази постулату робилися і в 19 ст. Тут слід зазначити роботи французького математика А. Лежандра; одне з його доказів (1800) засновано на припущенні, що через кожну точку всередині гострого кута можна провести пряму, що перетинає обидві сторони кута, т. е., як і всі його попередники, він замінив постулат ін. допущенням. Досить близько до побудови Л. р підійшли німецькі математики Ф. Швейкарт (1818) і Ф. Таурінус (1825), проте чітко висловленої думки про те, що запланована ними теорія буде логічно настільки ж досконала, як і геометрія Евкліда, вони не мали .
Питання про V постулаті Евкліда, що займав геометрів більше двох тисячоліть, було вирішено Лобачевским. Це рішення зводиться до того, що постулат не може бути доведений на основі ін. Посилок евклідової геометрії і що допущення постулату, протилежного постулату Евкліда, дозволяє побудувати геометрію настільки ж змістовну, як і евклидова, і вільну від протиріч. Лобачевський зробив про це повідомлення в 1826, а в 1829-30 надрукував роботу «Про початки геометрії» з викладом своєї теорії. У 1832 була опублікована робота угорського математика Я. Больяй аналогічного змісту. Як з'ясувалося згодом, німецький математик К. Ф. Гаусс також прийшов до думки про можливість існування несуперечливої неевклідової геометрії, але приховував її, побоюючись бути незрозумілим. Хоча Л. р розвивалася як умоглядна теорія і сам Лобачевський називав її «уявною геометрією», проте саме Лобачевський розглядав її не як гру розуму, а як можливу теорію просторових відносин. Однак доказ її несуперечності було дано пізніше, коли були вказані її інтерпретації і тим повністю вирішено питання про її реальному сенсі, логічної несуперечності.
Інтерпретації (моделі) геометрії Лобачевського. Л. р вивчає властивості «площині Лобачевського» (у планіметрії) і «простору Лобачевського» (у стереометрії). Площина Лобачевського - це площина (безліч точок), в якій визначено прямі лінії, а також руху фігур (разом з тим - відстані, кути та ін.), Що підкоряються всім аксіомам геометрії Евкліда, за винятком аксіоми про паралельних, яка замінюється вказаною вище аксіомою Лобачевського. Подібним чином визначається простір Лобачевського. Завдання з'ясування реального сенсу Л. р складалася в знаходженні моделей площині і простору Лобачевського, т. Е. В знаходженні таких об'єктів, в яких реалізувалися б відповідним чином витлумачені положення планіметрії і стереометрії Л. р (про інтерпретацію взагалі див. геометрія , Розділ Ілюмінація геометрії). Італійський математик Е. Бельтрами в 1868 зауважив, що геометрія на шматку площині Лобачевського збігається з геометрією на поверхнях постійної негативної кривизни, простий приклад яких представляє псевдосфера (Рис. 2). Якщо точкам і прямим на кінцевому шматку площині Лобачевського зіставляти точки і найкоротші лінії (геодезичні) на псевдосфері і руху в площині Лобачевського зіставляти переміщення фігури по псевдосфері з зігнутися, т. Е. Деформацією, що зберігає довжини, то всякій теоремі Л. р відповідатиме факт, який має місце на псевдосфері. Т. о., Л. р отримує простий реальний сенс. При цьому довжини, кути, площі розуміються в сенсі природного виміру їх на псевдосфері. Однак тут дається інтерпретація лише геометрії на шматку площині Лобачевського, а не на всій площині і тим більше не в просторі (в 1901 Д. Гільберт довів навіть, що взагалі в евклідовому просторі не може існувати регулярної поверхні, геометрія на якій збігається з геометрією всій площині Лобачевського).
У 1871 Ф. Клейн вказав ту модель як всій площині, так і простору Лобачевського, яка була описана вище і в якій площиною служить внутрішність круга, а простором - внутрішність кулі. Між іншим, в цій моделі відстань між точками (рис. 1) визначається як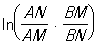 
; кут - ще складніше.
Пізніше А. Пуанкаре в зв'язку з завданнями теорії функцій комплексного змінного дав іншу модель. За площину Лобачевського приймається внутрішність круга (рис. 3), прямими вважаються дуги кіл, перпендикулярних колу даного круга, і його діаметри, рухами - перетворення, одержувані комбінаціями інверсій щодо кіл, дуги яких служать прямими. Модель Пуанкаре чудова тим, що в ній кути зображаються звичайними кутами. Виходячи з таких міркувань, можна будувати модель Л. р в просторі.
Коротко моделі Клейна і Пуанкаре можна визначити так. В обох випадках площиною Лобачевського може служити внутрішність круга (простором - внутрішність кулі), і Л. р є вчення про ті властивості фігур усередині круга (кулі), які в разі моделі Клейна не змінюються при проектних, а в разі моделі Пуанкаре - при конформних перетвореннях круга (кулі) самого в себе (проектні перетворення є ті, які переводять прямі в прямі, конформні - ті, які зберігають кути).
Можливо чисто аналітичне визначення моделі Л. р Наприклад, точки площині можна визначати як пари чисел х, у, прямі можна задавати рівняннями, рухи - формулами, зіставляти точкам (х, у) нові точки (х ', y'). Це буде абстрактно певна аналітична геометрія на площині Лобачевського, аналогічно аналітичній геометрії на площині Евкліда. Т. к. Лобачевський дав основи своєї аналітичної геометрії, то тим самим він вже фактично намітив таку модель, хоча повне її побудова з'ясувалося вже після того, як на основі робіт Клейна і інших виявилося само поняття про моделі. Інша аналітичне визначення Л. р полягає в тому, що Л. р визначається як геометрія ріманова простору постійної негативної кривизни (див. ріманови геометрії ). Це визначення було фактично дано ще в 1854 Б. Ріманом і включало модель Л. р як геометрії на поверхнях постійної кривизни. Однак Риму не пов'язав прямо своїх побудов з Л. р, а його доповідь, в якому він про них повідомив, не був зрозумілий і був опублікований лише після його смерті (в 1868).
Зміст геометрії Лобачевського. Лобачевський будував свою геометрію, вирушаючи від основних геометричних понять і своєї аксіоми, і доводив теореми геометричним методом, подібно до того, як це робиться в геометрії Евкліда. Основою служила теорія паралельних ліній, т. К. Саме тут починається відміну Л. р від геометрії Евкліда. Всі теореми, не залежні від аксіоми про паралельних, загальні обом геометрії та утворюють т. Зв. абсолютну геометрію, до якої відносяться, наприклад, теореми про рівність трикутників. Слідом за теорією паралельних будувалися ін. Відділи, включаючи тригонометрію і почала аналітичної та диференціальної геометрії. Наведемо кілька фактів Л. р, що відрізняють її від геометрії Евкліда і встановлених самим Лобачевським.
1) У Л. р не існує подібних, але нерівних трикутників; трикутники рівні, якщо їх кути рівні. Тому існує абсолютна одиниця довжини, т. Е. Відрізок, виділений за своїми властивостями, подібно до того як прямий кут виділений своїми властивостями. Таким відрізком може служити, наприклад, сторона правильного трикутника з даною сумою кутів.
2) Сума кутів всякого трикутника менше p і може бути як завгодно близькою до нуля. Це безпосередньо видно на моделі Пуанкаре. Різниця p - (a + b + g), де a, b, g - кути трикутника, пропорційна його площі.
3) Через точку О, що не лежить на даній прямій а, проходить нескінченно багато прямих, що не перетинають а й перебувають з нею в одній площині; серед них є дві крайні b, b ', які і називаються паралельними прямою а в сенсі Лобачевського. У моделях Клейна (Пуанкаре) вони зображуються хордами (дугами кіл), що мають з хордою (дугою) а загальний кінець (який за визначенням моделі виключається, так що ці прямі не мають спільних точок) (рис. 1,3). Кут її між прямою b (або b ') і перпендикуляром з Про на а - т. Зв. кут паралельності - у міру віддалення точки Про від прямої убуває від 90 ° до 0 ° (в моделі Пуанкаре кути в звичайному сенсі збігаються з кутами в сенсі Лобачевського, і тому на ній цей факт можна бачити безпосередньо). Паралель b з одного боку (а b 'з протилежною) асимптотика наближається до а, а з іншого - нескінченно від неї віддаляється (в моделях відстані визначаються складно, і тому цей факт безпосередньо не видно).
4) Якщо прямі мають загальний перпендикуляр, то вони нескінченно розходяться в обидві сторони від нього. До будь-якої з них можна відновити перпендикуляри, які не досягають іншої прямої.
5) Лінія рівних відстаней від прямій не є прямий, а особлива крива, звана еквідістантой, або гіперциклом.
6) Межа кіл нескінченно зростаючого радіусу не їсти пряма, а особлива крива, звана граничної окружністю, або орициклом.
7) Межа сфер нескінченно зростаючого радіусу не їсти площину, а особлива поверхня - гранична сфера, або орисфере; чудово, що на ній має місце евклідова геометрія. Це служило Лобачевському основою для виведення формул тригонометрії.
8) Довжина кола не пропорційно радіусу, а зростає швидше.
9) Чим менше область в просторі або на площині Лобачевського, тим менше геометричні співвідношення в цій області відрізняються від співвідношень евклідової геометрії. Можна сказати, що в нескінченно малої області має місце евклідова геометрія. Наприклад, чим менше трикутник, тим менше сума його кутів відрізняється від p; чим менше коло, тим менше відношення її довжини до радіусу відрізняється від 2 p, і т. п. Зменшення області формально рівносильно збільшенню одиниці довжини, тому при безмежному збільшенні одиниці довжини формули Л. р переходять у формули евклідової геометрії. Евклідова геометрія є в цьому сенсі «граничний» випадок Л. р
Л. р продовжує розроблятися багатьма геометрами; в ній вивчаються: рішення задач на побудову, многогранники, правильні системи фігур, загальна теорія кривих і поверхонь і т. п. Ряд геометрів розвивали також механіку в просторі Лобачевського. Ці дослідження не знайшли безпосередніх застосувань в механіці, але дали початок плідним геометричним ідеям. В цілому Л. р є великою областю дослідження, подібно геометрії Евкліда.
Додатки геометрії Лобачевського. Сам Лобачевський застосував свою геометрію до обчислення певних інтегралів. У теорії функцій комплексного змінного Л. р допомогла побудувати теорію автоморфних функцій . Зв'язок з Л. р була тут відправним пунктом досліджень Пуанкаре, який писав, що «неевклидова геометрія є ключ до вирішення всієї завдання». Л. р знаходить застосування також в теорії чисел, в її геометричних методах, об'єднаних під назвою «геометрія чисел» (див. чисел теорія ). Була встановлена тісний зв'язок Л. р з кінематикою спеціальної (приватної) теорії відносності (див. відносності теорія ). Цей зв'язок заснована на тому, що рівність, що виражає закон поширення світла
x2 + y2 + z2 = c2t2
при розподілі на t2, т. е. для швидкості світла, дає
vx2 + vy2 + vz2 = c2
- Рівняння сфери в пространстве з координатами vx, vy, vz - складового швідкості по осях х, у, z (у «пространстве швидкости»). Лоренца превращение зберігають Цю сферу І, т. к. смороду лінійні, що переводять Прямі простору швидкости в Прямі. Отже, відповідно до моделі Клейна, в просторі швидкостей усередині сфери радіусу з, т. Е. Для швидкостей, менших швидкості світла, має місце Л. р
Чудове додаток Л. р знайшла в загальній теорії відносності (див. тяжіння ). Якщо вважати розподіл мас матерії у Всесвіті рівномірним (це наближення в космічних масштабах допустимо), то виявляється, що при певних умовах простір має Л. р Т. о., Припущення Лобачевського про його геометрії як можливої теорії реального простору виправдалося.
Літ .: Лобачевський Н. І., Твори по геометрії, М. - Л., 1946-49 (Полн. Собр. Соч., Т. 1-3); Про підстави геометрії. Збірник класичних робіт по геометрії Лобачевського і розвитку її ідей, М., 1956; Александров П. С., Що таке неевклідова геометрія, М., 1950; Делоне Б. Н., Елементарне доказ несуперечності планіметрії Лобачевского, М., 1956; Широков П. А., Короткий нарис основ геометрії Лобачевського, М., 1955; Каган В. Ф., Лобачевський і його геометрія. Загальнодоступні нариси, М., 1955; його ж, Геометрія Лобачевського і її передісторія, М. - Л., 1949 (Підстави геометрії, ч. 1); Єфімов Н. В., Вища геометрія, 5 видавництво., М., 1971; Погорєлов А. В., Підстави геометрії, 3 вид., М., 1968; Розенфельд Б. А., Неевклідові простору, М., 1969; Нут Ю. Ю., Геометрія Лобачевського в аналітичному викладі, М., 1961; Андрієвська М. Г., Аналітична геометрія в просторі Лобачевського, К., 1963.
А. Д. Александров.
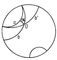
Мал. 3 до ст. Лобачевського геометрія.
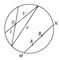
Мал. 1 до ст. Лобачевського геометрія.
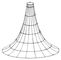
Мал. 2 до ст. Лобачевського геометрія.